Speed Governor and its Modeling

Speed Governor and its Modeling

Speed Governor

Speed governor is the automatic control system that controls the speed of the turbine-governor according to the load condition. The block diagram of the speed governor is shown above.

T_m = mechanical torque produced by turbine.

P_m = mechanical power input to the generator

T_e = electrical torque that opposes the mechanical torque.

P_e = electrical power output

At steady state,  P_m = P_e  

                          Also,    T_m = T_e ; at constant speed w₀

In the absence of the speed generator, the turbine-generator coupled system shows tendency to control the speed due to load variation to some extent and it is due to inertia. Mathematical expression can be generated during transient period, due to change in electrical load, the acceleration of deceleration of the  shaft is given from law of motion as;

            dw/dt = 1/2H×(T_m – T_e )   ----------------(1)

            where, H=inertia constant of turbine generator coupled system.

lets replace d/dt operator by ‘Δs’ in laplace domain

s.Δw = 1/2H× (T_m – T_e)

            Or,  Δw= 1/2Hs×((T_m – T_e)  ---------------------(2)

Equation 2 can be represented by following block diagram:

speed control by inertiaTurbine-Generator coupled system 

If change in the electrical load is significantly very large then the inertia of the turbine-generator system not sufficient to control the speed. In this case, a automatic speed governor is used

For a rotating system, power can be related with the speed as:

            P = wT   -------------------------------------(3)

Considering small change in power, speed and torque as ΔP, Δw, and ΔT respectively. Then equation  3 becomes:

            P+ΔP = (w₀+Δw)(T₀+ΔT)

            P+ΔP = w_0.T₀ + w₀.ΔT + Δw.T₀+Δw. ΔT

            ΔP = w₀. ΔT + Δw.T₀

Since, ΔP = ΔP_e - ΔP_m    

   So,    ΔP_e - ΔP_{m =} w₀.( ΔT_m – ΔT_e) + Δw(T_m – T_e)

At steady state;    T_m = T_e

            ΔP_e - ΔP_m  = w₀. (  ΔT_m – ΔT_e)

In pu system, when base speed is equal to initial speed, then w₀ = 1 pu.

ΔP_e - ΔP_m  = (  ΔT_m – ΔT_e)

In general, power system loads are composite in nature. Which is mixture of both resistive and inductive loads.

Inductive loads are frequency dependent. The frequency dependent loads produce damping effect to control the speed. Hence in general, power system loads can be represented as:

            ΔP_e = ΔP_L + D. Δw 

ΔP_e = ΔP_L + D. Δw 

Where, ΔP_L = frequency independent load

And        D. Δw = frequency dependent load whose effect comes into account only during transient period.

Where, D = load damping constant.

Load damping constant is defined as the % change in load for 1% change in frequency.

If we include the effect of load damping constant ‘D’, the block diagram will be:

block diagram of speed governor with damping constant 'D' 

The final Block Diagram of governor Modeling is:

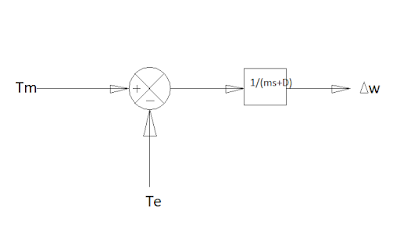The final Block diagram of Governor modeling